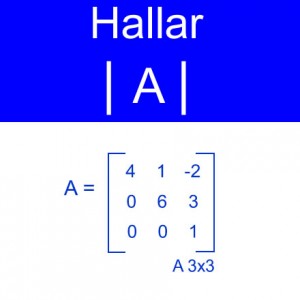
El problema planteado consiste en hallar el determinante de | A |, siendo A una matriz de orden 3×3 con A = [(4,1,-2),(0,6,3),(0,0,1)];
Esta solución hace uso de la teoría de álgebra lineal y las propiedades de calculo de determinantes. Toda matriz que sea triangular superior o inferior, el determinante será la suma del producto de los elementos de la diagonal principal.
Descargue aqui la solución y explicación completa de este ejercicio.
Nota: No todo calculo de determinantes por cofactores es eficiente a realizar con la primera fila, pues, es mas recomendable usar la fila con mayor cantidad de ceros ya que esto ahorraría calculo de operaciones aritméticas. Descargue aquí un ejemplo aplicativo.
[Tweet «»Una fila con muchos ceros alegra la vida si se trata de calcular el determinante.» #Tutorias ☺»]



