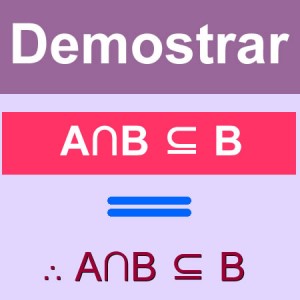
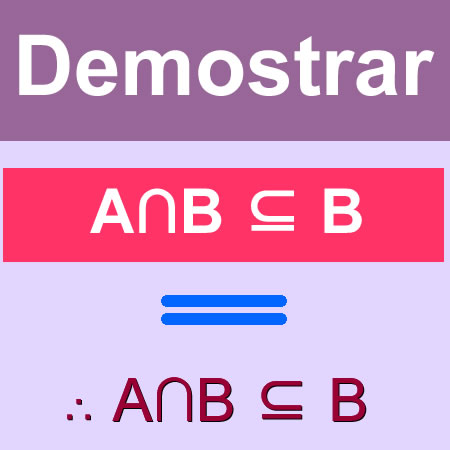
El problema planteado usar la teoría de conjuntos para demostrar como teorema que A ∩ B ⊆ B
Este ejercicio hace uso de la teoría de conjuntos teoremas y definiciones.
La demostración de conjuntos se apoya en las definiciones básicas y propiedades de conjuntos establecidas.
Intente resolver este ejercicio y luego compruebe la solucion. Descargue esta solucion clic aqui
∀x: x ∈ A∩B → x ∈ B Hipótesis y definición inclusión ∀x: (x ∈ A ∧ x ∈ B) → x ∈ B Definición intersección ∀x: (x∈A ∧ x∈B)∧ x∈B → x∈B ∧ x∈B Ley adición ∀x: (x∈A ∧ x∈B) → x∈B Idempotencia ∀x: x ∈ A∩B → x∈B Definición intersección A ∩ B ⊆ B ∴ A ∩ B ⊆ B