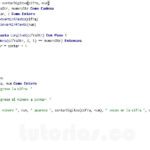
El problema planteado consiste en indicar el resultado en base octal de la multiplicación de los valores octales (7)8 * (7)8
Esta solución hace uso de la teoría de sistemas numéricos pesados. Se ve como multiplicando 1 dígito y como multiplicador 7. Como resultado del producto de cada multiplicador por la hilera superior se tiene: (61) como nuevas hileras y respetando las respectivas sangrías de ultima columna al sumar se obtiene: [61] 8
Para multiplicar bases octales hay que tener en cuenta el acarreo a llevar cuando se realice el producto de cada multiplicador por la hilera de multiplicandos, como la base octal va de [0..7] cuando el producto sobre pase el 7 entonces se resta la misma base hasta que de un valor octal y luego la cantidad de veces que se resto es el acarreo para sumar al resultando del proximo producto. Una vez se termine el producto de cada multiplicador por cada hilera entonces se realiza la respectiva suma de los octales. Hay que tener en cuenta que para sumar octales se suma digito por digito por columna de derecha a izquierda, tal cual como se hace con los números decimales. La base octal es de base ocho(8) y consta de 8 valores (0,1,…7). Si al sumar los dígitos el resultado sobrepasa la base (o sea 8) entonces se resta la misma base, tantas veces sea necesario hasta que el resultado no sobrepase la base y las veces que se resto es el acarreo para sumar en la siguiente columna. Si el acarreo es tres quiere decir que se resto tres veces la base (8) y por ende, se debe sumar 3 en la próxima columna. Ejemplo: Al sumar (4) + (4) en base octal el resultado sera (10) ya que la suma de la primera columna de derecha a izquierda es 8 y se resta la base dando 0 pero acarreando uno en la suma de la segunda columna. Como ya no hay columna que sumar entonces se pone el uno (acarreo) como ultimo valor.