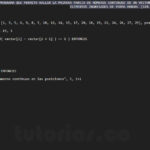
El problema planteado consiste en sumar la expresión de números enteros -{-[-[-(-3-1)]]}.
Esta solución hace uso de la teoría de suma de números enteros.
Para realizar sumas simples de números enteros se puede usar la técnica de suma por columnas alineando las cantidades hacia la derecha, sin embargo, una expresión agrupada se trata mas fácil resolviendo primero las agrupaciones mas internas teniendo en cuenta resolver el valor precedido del signo (-) y obteniendo así el resultado final. Para este ejercicio teniendo en cuenta la ley de signos es posible aplicar un truco y consiste simplemente en contar la cantidad de signos negativos que preceden la suma o el valor resultado y en caso de ser impar el signo del resultado sera negativo o en caso de ser par la cantidad de signos negativos, entonces el resultado será positivo, pero teniendo en cuenta también el signo de la suma.
Hay que tener en cuenta las propiedades de la suma de números enteros. En este caso la ley de signos y el resultado será un número entero debido a la propiedad clausurativa [Dado a,b ∈ Z entonces a+b ∈ Z]
¿Y cómo se realiza la suma?
Veamos. Se suman o restan valores agrupados para ir facilitando la suma.
-{-[-[-(-3-1)]]}
=-{-[-[-(-3-1)]]}
=-{-[-[-(-4)]]}
=-4


 eoria
eoria
Aclare algunos conceptos

 est
est
Tómese únicamente 90 segundos
Una buena practica para sumar números enteros es dejar un resultado con signo negativo en caso de obtenerse un valor negativo luego de la operación y de este modo evitar posibles errores de calculo.
[Tweet «»Los números positivos son llamados números naturales ya que pueden ser contados con la mano (naturaleza humana) y los números negativos junto a los positivos y el cero forman el conjunto de los números enteros.» #Tutorias ☺»]