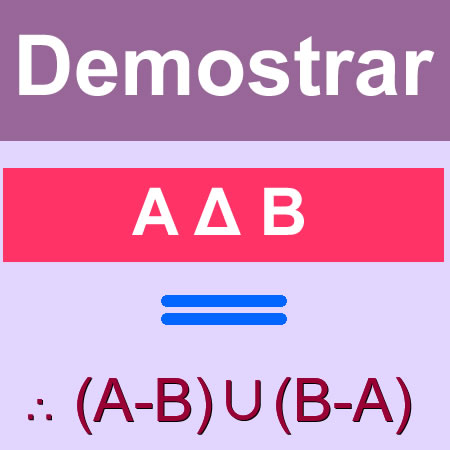
El problema planteado usar la teoría de conjuntos para demostrar como teorema que (AΔB) = (A-B) ∪ (B-A)
Este ejercicio hace uso de la teoría de conjuntos teoremas y definiciones.
La demostración de conjuntos se apoya en las definiciones básicas y propiedades de conjuntos establecidas.
Intente resolver este ejercicio y luego compruebe la solucion. Descargue esta solucion clic aqui
Sea x ∈ (AΔB) Definición general x ∈ (A∪B) ∧ x ∉ (A∩B) Definición diferencia simétrica (x ∈ A ∨ x ∈ B ) ∧ (x ∉ A ∧ x ∉ B ) Definición unión e intersección [[x∈A∧x∉A]∨[x∈B∧x∉A]] ∨ [[x∈A∧x∉B]∨[x∈B∧x∉B]] Ley distributiva conjunción [F ∨ [x∈B∧x∉A]] ∨ [[x∈A∧x∉B] ∨ F] Ley contradicción (x∉A ∧ x∈B) ∨ (x∈A ∧ x∉B) Ley idéntica disyunción (x∈A ∧ x∉B) ∨ (x∉A ∧ x∈B) Ley conmutativa disyunción [x ∈ (A-B)] ∨ [x ∈ (B-A)] Definición diferencia x ∈ (A-B) ∪ (B-A) Definición unión ∴ (AΔB) = (A-B) ∪ (B-A)
ESCUCHANDO
AMPLIAR ESCUCHANDO
Estoy para servirte y te digo que si te das cuenta de lo bonito, yo me doy cuenta que tienes el valor de la atención. Cuéntame como te puedo ayudar. Adelante, ¡ánimo!
Muy bonita la pagina y todo, pero para una persona con déficit de atención como yo es bastante complicado. Un abrazo