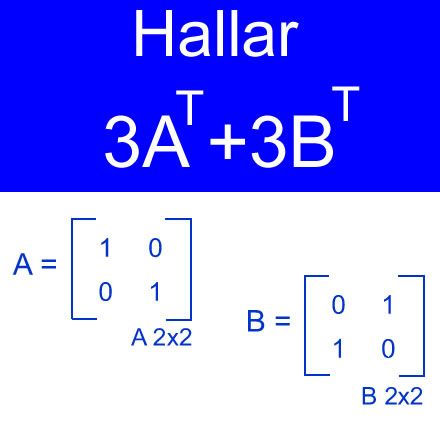
El problema planteado consiste en hallar la traspuesta de la matriz 3At+3Bt, siendo A,B matrices de orden 2×2 con A = [(1,0),(0,1)]; y B = [(0,1),(1,0)];
Esta solución hace uso de la teoría de álgebra lineal y las propiedades de las propiedades de traspuesta de matrices.
3AT + 3BT = [(3,3),(3,3)] 2×2
Descargue aqui la solucion completa de este ejercicio.
ESCUCHANDO
AMPLIAR ESCUCHANDO
[Tweet «»La traspuesta de una matriz identidad es la misma matriz y la traspuesta de una matriz secundaria es tambien la misma matriz» #Tutorias ☺»]