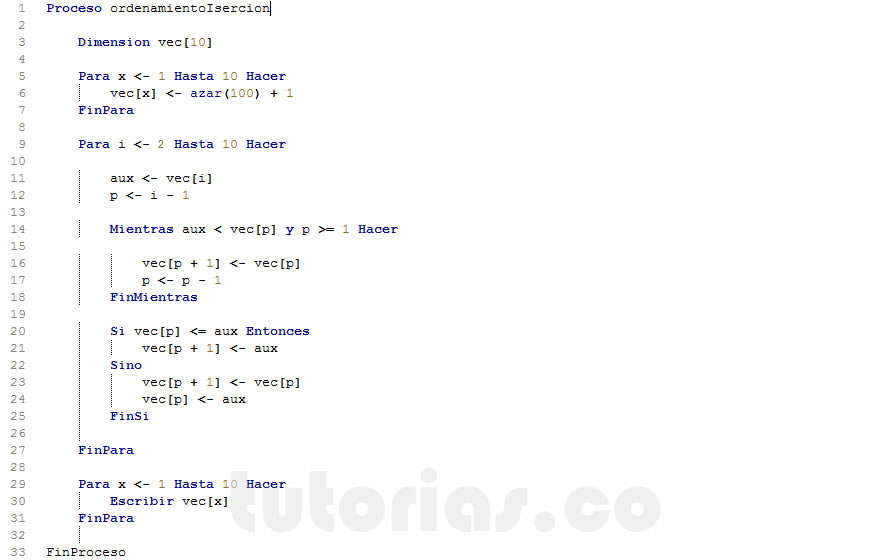
El problema planteado consiste en ordenar ascendentemente los datos de un vector usando el método de ordenamiento inserción.
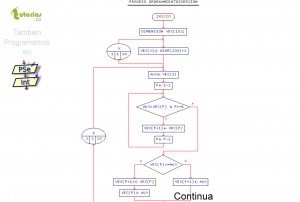
Este algoritmo hace uso de un ciclo mientras y un ciclo para. Este programa esta resuelto en pSeint y se genero el respectivo diagrama de flujo.
Para ordenar un conjunto de datos es necesario usar uno de los métodos universalmente conocidos como métodos de ordenamiento. Entre los mas conocidos estan: selección, quicksort, inserción, shell y burbuja.
Este ejercicio resuelve el ordenamiento de un vector por el método de ordenamiento inserción o también llamado de baraja.
La lógica de este algoritmo es comparar cada valor del vector con sus posteriores y luego ubicar en la posición acorde a su valor. El funcionamiento es similar como cuando usted juega cartas, en donde busca ordenar sus cartas de menor a mayor, ubicando cada una en el lugar correcto.
Un método de ordenamiento se puede implementar en cualquier estructura de datos estática o dinámica, es decir, se pueden ordenar listas ligadas, grafos, archivos planos, etc…

Quiero hacer este programa… Pero ¿Cómo funciona?
La ejecución paso a paso del programa la puede ver en la

 eoria
eoria
Aclare algunos conceptos

 est
est
Tómese únicamente 90 segundos

 ablero
ablero
Comparte tu Algoritmo
El uso de estructuras de datos, en este caso un array unidmiensional o vector, demanda acceso a la memoria RAM.
[Tweet «»Más que saber reservar memoria hay que evitar el desbordamiento de ésta. #Tutorias» ☺»]
Para ordenar un conjunto de datos usamos uno de los métodos de los tradicionalmente llamados métodos de ordenamiento. En este caso el método de ordenamiento inserción. Recuerde para las estructuras estáticas debe tener en cuenta que está reservando espacio estático de memoria ram, mientras que en las dinamicas puede separar cuanto necesite preocupándose solamente con no bloquear el programa por consumir toda la memoria RAM.