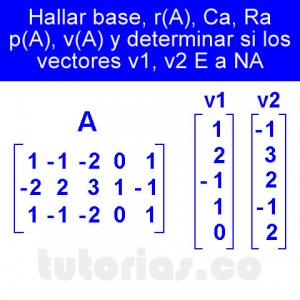
El problema planteado consiste en hallar base, r(A), Ca, Ra p(A), v(A) de una matriz 5×3.
Esta solución hace uso de la teoria de espacios de algebra lineal.
Para la resolución de este ejercicio es necesario tener en claro los conceptos de espacio nulo NA, nulidad r(A), imagen Im(A) y base de un espacio vectorial así mismo, los teoremas que los involucran.
Un espacio nulo (NA) es uno o un conjunto de vectores que anula la matriz, es decir, los vectores solución de la matriz. Para que se entienda mejor, haga de cuenta la solución de las variables de una ecuación sencilla, pero en este caso por tratarse de matrices y espacios vectoriales, se hablara de vectores.
Una vez hallado el espacio nulo, se podrá hacer uso de los demas teoremas para el calculo de la nulidad,imagen, rango y base.
El espacio columnas cA y filas rA simplemente son las columnas y filas respectivamente de la matriz original.
clic aqui para descargar la solucion de este ejercicio.
[Tweet «»El producto de matrices son aplicaciones practicas al algebra lineal» #Tutorias ☺»]



