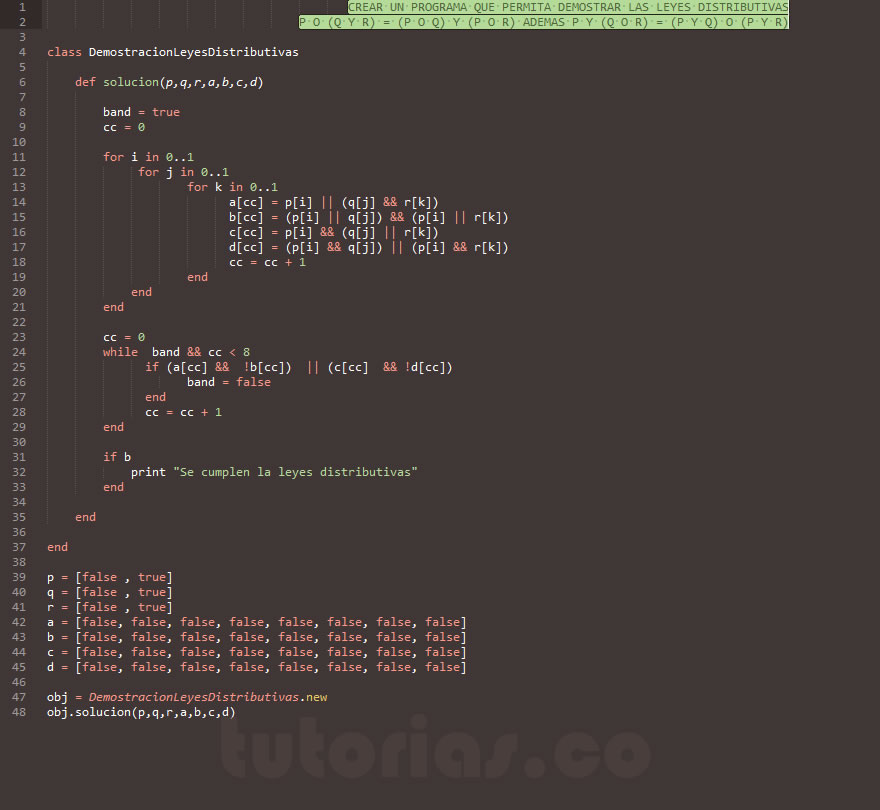
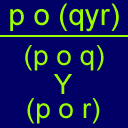El problema planteado se trata en demostrar las leyes distributivas lógicas: si P ó (Q y R) = (P ó Q) y (P ó R) además P y (Q ó R) = (P y Q) ó (P ó R)
El siguiente programa en ruby hace uso de POO (Programación Orientada a Objetos) y del ciclo for y de arrays (matrices)
La lógica que utiliza este programa en ruby es simple. Hace uso de las expresiones lógicas.

Quiero hacer este programa… Pero ¿Cómo funciona?
La ejecución paso a paso del programa la puede ver en la

 eoria
eoria
Aclare algunos conceptos

 est
est
Tómese únicamente 90 segundos

 ablero
ablero
Comparte tu Algoritmo
Recuerde que en las sentencias condicionales, puede ahorrar las comparaciones cuando use variables booleanas, pues la unidad logica las interpreta por su resultado, es decir, es mejor programar IF(variable) que programar IF(variable = True). Este programa puede ser modificado para demostrar la veracidad de cualquier ley logica.
[Tweet «»♥ is True or False» #Tutorias ☺»]